Statistics - Cybersecurity - Topics in Statistics

Statistics, Cybersecurity [Year 2020 - 21]

Topics on Statistics with intensive computer applications

$ \int_0^t d S_u = \int_0^t \mu(S_u, u) du + \int_0^t\sigma(S_u, u) dW_u $

Supporto al corso e alla didattica telematica, by T. Gastaldi #Sapienzanonsiferma #Sapienzadoesnotstop

(Instructor: tommaso.gastaldi@gmail.com,
https://www.datatime.eu/public/cybersecurity/)

Whatsapp group for the students of this course
Invitation to join the Whatsapp group for this course: https://chat.whatsapp.com/ELriCFo8aCW7lC6YwljuQGG
(work group for communication exchange about the course and exams. When first joining, send a message with your name and id ("matricola"))

Students research blogs: StudentsBlogs
each student will create his/her own free blog, eg. with any free blogging platform, to publish their hypertext essays [for the oral exam], and send me the link in the whatsapp group chat)

VOLUNTARY WORK GROUPS created by students

Work GROUP 1. ONLINE SURVEY (create entry form logic and dbms to collect anonymous exportable data from students of this course, for further processing within the course): https://www.isaacilliano.com/survey/ (to participate to the discussions of this group or contact the members: https://chat.whatsapp.com/C4QzASKowUSBxBlFZC6mUg )

WorkGROUP 2. ONLINE P2P BLOG POLL (an online P2P dynamic voting and reporting system to express personal preferences and likes about the students' blogs):
https://sites.google.com/view/statisticsonlineblogpoll/home (to participate to the discussions of this group or contact the members: https://chat.whatsapp.com/FPg66qdlMl60i6fHtbr1Ts )

Work GROUP 3. EXPERIMENTAL DISTRIBUTED P2P CROSS-GRADING SYSTEM FOR ONLINE HOMEWORKS (a prototype created by Cybersecurity students to grade the homeworks published online weekly). The grades are intended to reward: originality, clarity, accuracy, exhaustivity. (The system will not replace the instructor's grading work. However, it will be interesting to see how it correlates/compares with his work.). The system implements statistical methods, AI and advanced competitive logic to detect and penalize possible "collaborations" and alliances at any level or other factors which may compromise the process of a fair shared and distributed grading system.
https://statistics-grading-app.herokuapp.com/ (to participate to the discussions of this group or contact the members: https://chat.whatsapp.com/GTyVTXDmSAa0G5KUBiVw4f )

________________________________________________________________________________________

- LESSON 01 - [08 Oct 2020] (official start date for lessons is has been postponed again to 5/10, see: https://web.uniroma1.it/i3s/node/9341 )

STREAMING or VIDEOS LESSONS:

Course Introduction

Lesson_01_Intro_01_Welcome_CourseStructure_Exams https://drive.google.com/file/d/1OFWq9cpEyIfk7qcPBVF_kX1IILYVkn8m/view?usp=sharing

Lesson_01_Intro_02_OralExam_YourBlog https://drive.google.com/file/d/1_7tICctUq7lHXWTFjlHfgG_6kWvkuBxq/view?usp=sharing

Lesson_01_Intro_03_WrittenExam_YourIDE https://drive.google.com/file/d/1g6KQbvuNNwCEFdr0L0gebCNas1DfByAP/view?usp=sharing

Lesson_01_Intro_04_LessonWorkFlow_HowtoCiteYourSources https://drive.google.com/file/d/10ZiwDmOJelY4AmCKU0L8u9oII38VqcMl/view?usp=sharingg

Theory

Lesson_01_Theory_01_DataSetDefinition_Population_Attributes https://drive.google.com/file/d/1B1MUKNXEbrYmMuZTNPf-SObLwCxhD3Hp/view?usp=sharing

Lesson_01_Theory_02_DescriptiveAndInferentialStatistics https://drive.google.com/file/d/1C7JIf1d5a5W_Pa3M18Zp6WQqySESQFsN/view?usp=sharing

Lesson_01_Theory_03_UnivariateAndMultivariateStatistics https://drive.google.com/file/d/17kjGwE-S5NDuLhmQUcexvDXAyntireof/view?usp=sharing

Lesson_01_Theory_04_FirstUnivariateExample_TowardTheDistribution https://drive.google.com/file/d/1mEmOTQkJ4sX4pYB3OoxdrEVts0JD8YBS/view?usp=sharing

Lesson_01_Theory_05_ImportanceOfDistribution https://drive.google.com/file/d/18qR73tUfm9-Nm869UAAW12UvytKS4T0C/view?usp=sharing

Lesson_01_Theory_06_EmpiricalUnivariateDistribution https://drive.google.com/file/d/1WkQVYbkofjAQlChoWbPstEUT9p_QcUrL/view?usp=sharingg

Computer applications, and language fundamentals for statistical algos

Researches about theory (R)

1_R. Describe the notion of statistical population. What is a population in Descriptive Statistics and what is a population in Inferential Statistics: point out the differences.

2_R. Describe the notion of statistical attributes/variables and dataset, and explain how a dataset is generated.

3_R. Explain the differences between a (univariate) dataset and a (univariate) frequency distribution. Given a distribution can we reconstruct the dataset? why ?
How would you describe the change of amount of information passing from the dataset to the distribution?

Applications / Practice (A)

1_A. Create - in both languages C# and VB.NET - a program which does the following simple tasks:

when a button is pressed some text appears in a richtexbox on the startup form
when another button is pressed the richtextbox is cleared
when the mouse enters the richtextbox, the richtext backcolor is switched to another color
when the mouse leaves the richtextbox, the richtext backcolor is reset to its original state

2_A. Create or search, in both languages C# and VB.NET, some simple but illuminating example of code which clearly shows the different behaviors of reference value data types and value type data types.

3_A. Search on the web how to drag drop the name (its full path) of any file into a richtextbox on your startup form and try to implement this feature in your first program in both languages C# and VB.NET (e.g., https://stackoverflow.com/questions/11686631/drag-drop-and-get-file-path-in-vb-net , https://support.microsoft.com/en-us/help/307966/how-to-provide-file-drag-and-drop-functionality-in-a-visual-c-applicat , https://stackoverflow.com/questions/8550937/c-sharp-drag-and-drop-files-to-form ).

Researches about applications (RA)

1_RA. Observe carefully the different way C# and VB.NET deals with events and the different ways to define the event handlers. Discuss in your blog what differences you can spot. Which way do you find easier or more comfortable and why ?

2_RA. Note that any C# will have a Program.cs file in its solution folder while VB.NET does not. On the other hand, VB.NET has the file Application.Designer.vb within the project folder. Try to research what these (automatically created) files are doing in your application and try to discover / reverse engineer the differences on how a C# and VB.NET program are started.

REFERENCES / SOURCES / USEFUL LINKS:

Platform to publish your weekly homework:

Choose your free blogging platform: https://www.wpbeginner.com/beginners-guide/how-to-choose-the-best-blogging-platform/ , https://www.creativebloq.com/web-design/best-blogging-platforms-121413634
Always cite your sources and give proper credits (this is useful for both avoiding plagiarism, but also declining responsibility for possible errors in the sources): https://www.plagiarism.org/article/how-do-i-cite-sources

For applications:

Download your IDE (include C# and VB.NET): https://visualstudio.microsoft.com/it/downloads//
Example of VB.NET c# comparison table: https://sites.harding.edu/fmccown/vbnet_csharp_comparison.html
Example of code converter: https://codeconverter.icsharpcode.net/
Case styles: https://medium.com/better-programming/string-case-styles-camel-pascal-snake-and-kebab-case-981407998841
Format Shortcut: https://stackoverflow.com/questions/4942113/is-there-a-format-code-shortcut-for-visual-studio#:~:text=To%20answer%20the%20specific%20question,F%20to%20format%20the%20selection

Programming paradigms, OOP: https://en.wikipedia.org/wiki/Programming_paradigm
Event driven programming: https://en.wikipedia.org/wiki/Event-driven_programming
Object class: https://docs.microsoft.com/en-us/dotnet/api/system.object?view=netcore-3.1
Inheritance: https://medium.com/@andrewkoenigbautista/inheritance-in-object-oriented-programming-d8808bca5021
Value types vs Reference types: https://docs.microsoft.com/it-it/dotnet/csharp/language-reference/builtin-types/value-types , http://net-informations.com/faq/general/valuetype-referencetype.htm , https://www.c-sharpcorner.com/article/C-Sharp-heaping-vs-stacking-in-net-part-i/ , https://www.codeproject.com/Articles/1204612/How-string-Behaves-Like-Value-Type-as-it-is-refere
Value type: https://docs.microsoft.com/it-it/dotnet/api/system.valuetype?view=netcore-3.1

For Blogs:

https://www.websiteplanet.com/blog/business-blogging-statistics/

______________________________________________________________________________________

- LESSON 02 - [15 Oct 2020]

STREAMING or VIDEOS LESSONS:

Theory

Lesson_02_Theory_01_AttributeOperationalization_ScaleOfMeasurement https://drive.google.com/file/d/1MotGvQALCv0RSI9m_qU3SBckHZb3m7cF/view?usp=sharing

Lesson_02_Theory_02_CategoricalAndQuantitativeVariables https://drive.google.com/file/d/1ehacAHXb5eaBN99l_1siNHj_3huHUfBY/view?usp=sharing

Lesson_02_Theory_03_TimeSeriesAnalysis https://drive.google.com/file/d/1-IJ280tHTn78Le8vpiAItvO9eO80cjs1/view?usp=sharing

Lesson_02_Theory_04_SpacialDataAnalysis https://drive.google.com/file/d/1UFGQ3arfpeHFYgiIx0FvqXF0cqrVwLIX/view?usp=sharing

Lesson_02_Theory_05_StatisticalDataInRealWorld_DW_OLTP_Olap https://drive.google.com/file/d/1WMI-N4Swi6lnXWD7KHYOLE_Yvp8RGtwX/view?usp=sharing

Lesson_02_Theory_06_StreamAndBatchProcessing_Intro_DataStreaming https://drive.google.com/file/d/1pVZZ23inf5wFiFsop1y-ZY4zoj9ebeKD/view?usp=sharing

Lesson_02_Theory_07_StreamAndBatchProcessing_Intro_OnlineOffline https://drive.google.com/file/d/115LNBHnjQfUYPDFJOOToGVEHxEKUNS0e/view?usp=sharing

Lesson_02_Theory_08_StreamAndBatchProcessing_Intro_Collections_Random_Timer https://drive.google.com/file/d/1-nxFZ488KyyRoSLqstxnTS06FWuw9kjy/view?usp=sharing

Lesson_02_Theory_09_StreamAndBatchProcessing_Intro_AverageAsRepresentativeValue https://drive.google.com/file/d/1oOnXX9W7gWkUchTpYXKPvxmMQ3L-mpEl/view?usp=sharing

Lesson_02_Theory_10_StreamAndBatchProcessing_Intro_Metadata https://drive.google.com/file/d/1nysLtwfxahZyagsLeA_S85_4BOYpWdEo/view?usp=sharing

Lesson_02_Theory_11_StreamAndBatchProcessing_Intro_RawDataToObjects https://drive.google.com/file/d/1wLmmIesCiFdOkkMLZmChEibryfnLKmni/view?usp=sharing

Lesson_02_Theory_12_StreamAndBatchProcessing_KnuthOnlineAlgo https://drive.google.com/file/d/1LmzG2uKSO4X782XQ8w0n57emJxXxHirl/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

Lesson_02_Apps_01_StreamAndBatchProcessing_BatchExample_Random_List https://drive.google.com/file/d/1AazPlPpEwo35DQkT7_xgLKuriGRgiSue/view?usp=sharing

Lesson_02_Apps_02_StreamAndBatchProcessing_StreamExample_OnlineAlgo https://drive.google.com/file/d/14i5P3-FBagNwyRLx36Xhdofo2AWmiJ-h/view?usp=sharing

Lesson_02_Apps_03_ImportanceOfMeanOnlineAlgo_IssuesWithFloatingPoint https://drive.google.com/file/d/1iApjQUliWs8Qm66yfVqzLSwFRE9-w7rq/view?usp=sharing

Lesson_02_Apps_04_UnivariateDistribution_DiscreteVariable https://drive.google.com/file/d/14RNJguDeBaw0EXi4H2H64eyzmFRddDt3/view?usp=sharing

Lesson_02_Apps_05_UnivariateDistribution_ContinuousVariable https://drive.google.com/file/d/1XelrkJC8qfDycuNmWkZNd5vEsMco7xjJ/view?usp=sharing

Extra help to clean up code (optional videos):

OPT Lesson_02_Apps_06_RefactoringExample_NeedForModularity https://drive.google.com/file/d/1wOT7fn60ndCOvVsOR9T4IUTD47fRYTsh/view?usp=sharing

OPT Lesson_02_Apps_07_RefactoringExample_Maintanability https://drive.google.com/file/d/1ne8uwE5oYW7GwuqZWoTYXgnFKM0pN5mR/view?usp=sharing

OPT Lesson_02_Apps_08_RefactoringExample_Linq_LambdaExpressions https://drive.google.com/file/d/1mtv9UT6azakrQFZlbqSyUHFyyCHW6TMU/view?usp=sharing

OPT Lesson_02_Apps_09_RefactoringExample_Reusability https://drive.google.com/file/d/1ISl9eK3QPBb1vrn7pj2yHLLtAEUmYgxk/view?usp=sharing

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 21 Oct 2020 or -1 penalty on final grade may apply]

Researches about theory (R)

4_R. A characteristic (or attribute or feature or property) of the units of observation can be measured and operationalized on different "levels", on a given unit of observation, giving rise to possible different operative variables. Find out about the proposed classifications of variables and express your opinion about their respective usefulness (e.g., https://en.wikipedia.org/wiki/Level_of_measurement , https://www.youtube.com/watch?v=eghn__C7JLQ , https://www.youtube.com/watch?v=jigW0a8cC5c , etc.)

5_R. Describe the most common configuration of data repositories in the real world and corporate environment. Concepts such as Operational or Transactional systems (OLTP), Data Warehouse DW, Data Marts, Analytical and statistical systems (OLAP), etc. Try to draw a conceptual picture of how all these components may work together and how the flow of data and information is processed to extract useful knowledge from raw data.

6_R. Show how we can obtain an online algo for the arithmetic mean and explain the various possible reasons why it is preferable to the "naive" algo based on the definition.

Applications / Practice (A)

4_A. Create - in both languages C# and VB.NET - a demonstrative program which computes the online arithmetic mean (if it's a numeric variable) and the distribution for a discrete variable (can use values simulated with RANDOM object).

5_A. Create - in your preferred language C# or VB.NET - a demonstrative program which computes the online arithmetic mean (or "running mean") and distribution for a continuous variable (can use random simulated values). Make the code as general and reusable as possible, as it must be used in your next applications and exam.

(In both exercises, create your own algorithm, by either inventing it from scratch based on your own ideas, or putting it together by researching everywhere, striving for the most usable and general logic, good efficiency and numerical stability)

6_A. Create one or more simple sequences of numbers which clearly show the problem with the "naive" definition formula of the arithmetic mean, and explore possible ways to fix that.
Provide alternative algorithms to minimize problems with the floating point representation with simple demos with actual numbers. ( https://en.wikipedia.org/wiki/Kahan_summation_algorithm , https://stackoverflow.com/questions/1930454/what-is-a-good-solution-for-calculating-an-average-where-the-sum-of-all-values-e , https://stackoverflow.com/questions/23813278/how-to-compute-mean-average-robustly , https://www.drdobbs.com/floating-point-summation/184403224 , etc. )

Researches about applications (RA)

3_RA. Understand how the floating point representation works and describe systematically (possibly using categories) all the possible problems that can happen. Try to classify the various issues and limitations (representation, comparison, rounding, propagation, approximation, loss of significance, cancellation, etc.) and provide simple examples for each of the categories you have identified (e.g., https://floating-point-gui.de/basic/ , https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html , http://indico.ictp.it/event/8344/session/50/contribution/207/material/slides/0.pdf , https://stackoverflow.com/questions/2100490/floating-point-inaccuracy-examples , etc.)

REFERENCES / SOURCES / USEFUL LINKS:

For applications

Collections and Data Structures: https://docs.microsoft.com/en-us/dotnet/standard/collections/
https://stackoverflow.com/Questions/128636/net-data-structures-arraylist-list-hashtable-dictionary-sortedlist-sorted
https://stackoverflow.com/questions/1427147/sortedlist-sorteddictionary-and-dictionary

List: https://www.dotnetperls.com/list-vbnet , http://vb.net-informations.com/collections/list.htm
Dictionary: https://www.tutorialsteacher.com/csharp/csharp-dictionary , http://vb.net-informations.com/collections/dictionary.htm
Sorted Dictionary: https://docs.microsoft.com/it-it/dotnet/api/system.collections.generic.sorteddictionary-2?view=netcore-3.1 , https://www.dotnetperls.com/sorteddictionary
Sorted List: https://docs.microsoft.com/it-it/dotnet/api/system.collections.sortedlist?view=netcore-3.1 , https://www.tutorialsteacher.com/csharp/csharp-sortedlist , https://www.dotnetperls.com/sortedlist-vbnet
KeyValuePair: https://docs.microsoft.com/en-us/dotnet/api/system.collections.generic.keyvaluepair-2?redirectedfrom=MSDN&view=netcore-3.1

Floating point: https://en.wikipedia.org/wiki/Floating-point_arithmetic , https://stackoverflow.com/questions/18409496/is-it-52-or-53-bits-of-floating-point-precision
Floating point issues: https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html , https://www.volkerschatz.com/science/float.html , https://floating-point-gui.de/ , https://csharpindepth.com/Articles/FloatingPoint .
Decimal floating point: https://csharpindepth.com/Articles/Decimal , https://stackoverflow.com/questions/618535/difference-between-decimal-float-and-double-in-net
Loss of significance, catastrophics cancellation: https://en.wikipedia.org/wiki/Loss_of_significance
Fixing sums: https://en.wikipedia.org/wiki/Kahan_summation_algorithm
Integer division: https://stackoverflow.com/questions/661028/how-can-i-divide-two-integers-to-get-a-double

For/For each loop: https://www.tutorialsteacher.com/csharp/csharp-for-loop
Do Loop: https://www.tutorialsteacher.com/csharp/csharp-do-while-loop
If Then Else: https://www.tutorialspoint.com/vb.net/vb.net_if_else_statements.htm , https://www.dotnetperls.com/if-vbnet

My quick summary of control structures (ita): StruttureControlloFlusso.txt (send changes if you see inaccuracies, things to add/improve)

Reusability, Maintanability, Modularity, Performance: https://en.wikipedia.org/wiki/Reusability, http://singlepageappbook.com/maintainability1.html#:~:text=Modular%20code%20is%20code%20which,not%20just%20about%20code%20organization . https://press.rebus.community/programmingfundamentals/chapter/modular-programming/ , https://stackoverflow.com/questions/1444221/how-to-make-code-modular , https://en.wikipedia.org/wiki/Modular_programming , http://www.jrobbins.org/ics121f03/lesson-maintain.html , https://softwareengineering.stackexchange.com/questions/279140/performance-versus-reusability , ...

LINQ: https://docs.microsoft.com/en-us/dotnet/csharp/programming-guide/concepts/linq/ , https://www.tutorialsteacher.com/linq/linq-query-syntax , https://www.tutorialsteacher.com/linq/linq-method-syntax
Lambda expressions: https://www.tutorialsteacher.com/linq/linq-lambda-expression

Murphy Law: https://en.wikipedia.org/wiki/Murphy%27s_law
Spaghetti code: https://en.wikipedia.org/wiki/Spaghetti_code

_______________________________________________________________________________________

- LESSON 03 - [22 Oct 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT" denotes homework that can be skipped.

Theory

Lesson_03_Theory_01_BivariateDistribution_Marginal_Conditional https://drive.google.com/file/d/1wgn-MDiG9H1FKFibCcTKyaTwYhSiKl-o/view?usp=sharing

Lesson_03_Theory_02_BivariateDistribution_ContingencyTable https://drive.google.com/file/d/1fo1xsPRNzrhmNThHN_NHXjozC3vFEfLU/view?usp=sharing

Lesson_03_Theory_03_BivariateDistribution_Bayes https://drive.google.com/file/d/1s6sf8JJJh_UsBs86TxON3uEt4udSEv-u/view?usp=sharing

Lesson_03_Theory_04_BivariateDistribution_StatisticalIndependence https://drive.google.com/file/d/1AK98i1qehD3CrvbEkYAb-0tiLuCpCtzf/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

OPT Lesson_03_Apps_01_ReadingExternalDataSources_Intro https://drive.google.com/file/d/1WfqUhl_dftfnibnK_seLPFa-J39p8GFi/view?usp=sharing

Lesson_03_Apps_02_StreamReader_Field_Parser_FileDialog https://drive.google.com/file/d/1Woj01dQ8s_Ia2bUm6YdqiAGQa0yeaDHE/view?usp=sharing

Lesson_03_Apps_03_ReadingCSV_Example https://drive.google.com/file/d/1pkU4hwpIoSmTAwh04yI335kKfdonpdAr/view?usp=sharing

OPT Lesson_03_Apps_04_GeneralizingProgramsWithReflection https://drive.google.com/file/d/1-fqU1fc8rVYSDFsQO_Oyh0QuwL0sflFt/view?usp=sharing

OPT Lesson_03_Apps_05_BivariateDistribution_DiscreteVariable_GettingReady https://drive.google.com/file/d/1_Nawbiqw59aXPQ6R1TOXOT0Jo7WuLxdj/view?usp=sharing

Lesson_03_Apps_06_BivariateDistributionDiscrete_Computing https://drive.google.com/file/d/1aZZ8ZTVrgqLGwlnmTK5Tz38JjDgcYT_j/view?usp=sharing

OPT Lesson_03_Apps_07_BivariateDistributionDiscrete_MakingTheContingencyTable https://drive.google.com/file/d/1VK3_qX5T8FBHiLNkouzGhJPc6rr0KVc7/view?usp=sharing

OPT Lesson_03_Apps_08_BivariateDistributionDiscrete_MoreDetails_Hashset_SortedSet https://drive.google.com/file/d/10x_znFTmastvqai9Bw17VT1hkYPR8uRa/view?usp=sharing

Lesson_03_Apps_09_BivariateDistribution_ClassInterval https://drive.google.com/file/d/1JBRpM0CvMMZZ1f78Z7dmNp80JOrGcyeg/view?usp=sharing

Lesson_03_Apps_10_QuickIntroductionToGraphics https://drive.google.com/file/d/1PRTrnKlvbeCYWJ9S-hRSiJfEC8LFsPAi/view?usp=sharing

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 28 Oct 2020 or -1 penalty on final grade may apply]

Researches about theory (R)

7_R. Explain what are marginal, joint and conditional distributions and how we can explain the Bayes theorem using relative frequencies.

8_R. Explain the concept of statistical independence and why, in case of independence, the relative joint frequencies are equal to the products of the corresponding marginal frequencies..s.

9_R. Do a review about charts useful for statistics and data presentation (example of some: StatCharts.txt ). What is the chart type that impressed you most and why ?

Applications / Practice (A) [work on this at least 30' a day, all days]

7_A. Create - in your preferred language C# or VB.NET - a program which is able to read ANY file CSV (or at least 99% of them), assuming no prior knowledge about its structure (do not even assume to that a first line with variable names is necessarily present in the CSV: when not present, clearly, do some useful automatic naming). The program should use your intelligence, creativity and data checking functions (see references below) to achieve this task. The GUI should display the variables in a control, such as for instance a Treeview (or anything you deem useful, eg, https://docs.microsoft.com/en-us/dotnet/api/system.windows.forms.treeview?view=netcore-3.1 ) and let the user select the data type for each field in the CSV files. Also, some data preprocessing should be carried out on the data (or a suitable subset) in order to empirically establish the most suitable type of data of each field and, thus, give a preliminary tentative choice of data types for the variable fields to the program user (which he can, then, try to change on the GUI at his will before attempting to read the file) eg., https://stackoverflow.com/questions/5311699/get-datatype-from-values-passed-as-string/5325687 , https://stackoverflow.com/questions/4208244/get-current-language-in-cultureinfo , https://docs.microsoft.com/it-it/dotnet/api/system.globalization.cultureinfo.currentculture?view=netcore-3.1 ). Test the program with several CSV files downloaded from the Internet from various languages (ita, es/us, cn, ...) (eg, https://www.stats.govt.nz/large-datasets/csv-files-for-download/ , https://data.world/datasets/csv , https://support.spatialkey.com/spatialkey-sample-csv-data/ ) to make that values are parsed as intended. (For specific date field, the GUI could also let the user specify a custom format in a textbox to read it correctly https://stackoverflow.com/questions/919244/converting-a-string-to-datetime )

[Some hints for the exercise 7_A:
To hold information about variables (columns of the CSV file), you might create a suitable data structure of objects each of which represents all the info (eg, name, inferred data type, user selected data type, and so on) gathered about each variable.
To hold the values of each data point (rows of the CSV file), you might define an object which will hold the collection of values, for the respective variables, of each data point. Be careful about missing data. In case you need to catch and process exceptions, you may use the TRY CATCH structure: https://docs.microsoft.com/en-us/dotnet/standard/exceptions/best-practices-for-exceptions ]

OPT 8_A. In the previous program 7_A, as a verification, plug the code you have already developed for computing the mean and the (univariate) statistical distribution, and allow the user to select any variable and compute the arithmetic mean (only when it makes sense) and the distribution. [Make this general enough, in anticipation of next homework program, where we will also add bivariate distributions and, in general, multivariate distributions, with various charts.]

Researches about applications (RA)

4_RA. Find on the internet and document all possible ways you can infer a suitable data type, useful for statistical processing, when you are getting data points as a flow of alphanumeric strings ( https://en.wikipedia.org/wiki/Alphanumericc , https://stackoverflow.com/questions/5311699/get-datatype-from-values-passed-as-string/5325687. Be aware of possible format difference due to language.)

5_RA. Do a research about Reflection and the type Type and make all examples that you deem to be useful. (eg,. http://csharp.net-tutorials.com/reflection/introduction/n/ http://www.codeproject.com/Articles/17269/Reflection-in-C-Tutorial http://www.codeguru.com/csharp/csharp/cs_misc/reflection/article.php/c4257 http://www.youtube.com/watch?v=C-G7fobbBP0 http://www.codeproject.com/Articles/55710/Reflection-in-NET , etc.

6_RA. Do a comprehensive research about the GRAPHICS (GDI+ library) object and all its members.

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on statistical theory:

Bivariate distribution: http://www.brainkart.com/article/Bivariate-Frequency-Distributions_35069/#:~:text=In%20other%20words%2C%20a%20bivariate,students%20in%20an%20intelligent%20test.&text=Each%20cell%20shows%20the%20frequency%20of%20the%20corresponding%20row%20and%20column%20values.

Contingency table: https://en.wikipedia.org/wiki/Contingency_table

Conditional relative frequency: https://www.youtube.com/watch?v=PHORXJSIm2k
Bayes: https://www.youtube.com/watch?v=XQoLVl31ZfQ , https://betterexplained.com/articles/understanding-bayes-theorem-with-ratios/
Independence: https://www.youtube.com/watch?v=ZxzVfRiitM0

For applications

CSV: https://en.wikipedia.org/wiki/Comma-separated_values, https://tools.ietf.org/html/rfc4180 , https://www.loc.gov/preservation/digital/formats/fdd/fdd000323.shtml , https://www.thoughtspot.com/6-rules-creating-valid-csv-files

StreamReader: https://www.dotnetperls.com/streamreader, https://www.tutorialspoint.com/vb.net/vb.net_text_files.htm
TextFieldParser: https://docs.microsoft.com/it-it/dotnet/api/microsoft.visualbasic.fileio.textfieldparser?view=netcore-3.1 , https://stackoverflow.com/questions/22297562/csv-text-file-parser-with-textfieldparser-malformedlineexception
StreamWriter: https://www.dotnetperls.com/streamwriter-vbnet

HashSet https://docs.microsoft.com/it-it/dotnet/api/system.collections.generic.hashset-1?view=netcore-3.1
SortedSet https://docs.microsoft.com/it-it/dotnet/api/system.collections.generic.sortedset-1?view=netcore-3.1
Tuple: https://docs.microsoft.com/it-it/dotnet/api/system.tuple-2?view=netcore-3.1

Interface, Multiple inheritance: https://www.ict.social/vbnet/oop/interfaces-in-vbnet-course
Icomparable https://docs.microsoft.com/it-it/dotnet/api/system.icomparable?view=netcore-3.1

Type class: https://docs.microsoft.com/en-us/dotnet/api/system.type?view=netcore-3.13.1
GetType / typeof http://net-informations.com/q/faq/type.html

Isnumeric: https://docs.microsoft.com/it-it/office/vba/language/reference/user-interface-help/isnumeric-function , https://stackoverflow.com/questions/894263/identify-if-a-string-is-a-number , https://docs.microsoft.com/it-it/dotnet/csharp/programming-guide/strings/how-to-determine-whether-a-string-represents-a-numeric-value

Number/String checks: https://stackoverflow.com/questions/5311699/get-datatype-from-values-passed-as-string/5325687 , https://stackoverflow.com/questions/2751593/how-to-determine-if-a-decimal-double-is-an-integer , https://www.codeproject.com/Articles/13338/Check-If-A-String-Value-Is-

Parse datetime:https://stackoverflow.com/questions/919244/converting-a-string-to-datetimee, https://docs.microsoft.com/it-it/dotnet/api/system.datetime.parseexact?view=netcore-3.1 , http://net-informations.com/q/faq/stringdate.html , https://docs.microsoft.com/en-us/dotnet/standard/base-types/standard-date-and-time-format-strings?redirectedfrom=MSDN

Reflection: https://docs.microsoft.com/it-it/dotnet/visual-basic/programming-guide/concepts/reflection , https://docs.microsoft.com/it-it/dotnet/standard/attributes/retrieving-information-stored-in-attributes , http://net-informations.com/faq/net/reflection.htm , https://www.codemag.com/Article/0211161/Reflection-Part-1-Discovery-and-Execution , https://www.youtube.com/watch?v=4Xt2o3oQMD0 , https://www.youtube.com/watch?v=wfDFI9A56Gs

Asymptotic computational complexity: https://en.wikipedia.org/wiki/Asymptotic_computational_complexity#:~:text=In%20computational%20complexity%20theory%2C%20asymptotic,of%20the%20big%20O%20notation. , https://en.wikipedia.org/wiki/Big_O_notation

Graphics object: https://docs.microsoft.com/en-us/dotnet/desktop/winforms/advanced/getting-started-with-graphics-programming?view=netframeworkdesktop-4.8
Transforms: http://math.hws.edu/graphicsbook/c2/s1.html , http://math.hws.edu/graphicsbook/c2/s3.html ,
Charts: https://en.wikipedia.org/wiki/Chart , https://visme.co/blog/types-of-graphs/ , https://www.fusioncharts.com/charts/gauges

Statistical data presentation: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5453888/

_______________________________________________________________________________________

- LESSON 04 - [29 Oct 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT" denotes homework that can be skipped.

Theory

Lesson_04_Theory_01_MeasuresOfCentralTendency_Dispersion https://drive.google.com/file/d/1nbxS0IDwvedWQYv9JKxczwBYCHdAdglw/view?usp=sharing

Lesson_04_Theory_02_OnlineAlgoForVariance_Welford https://drive.google.com/file/d/1PN6TYEH4XO6NsYF2-9o6aZrRIYXYmkUC/view?usp=sharing

Lesson_04_Theory_03_Covariance_OnlineAlgo https://drive.google.com/file/d/1XcZXbrtPM-fmi3gJ0Zp72Qry7NO_sppx/view?usp=sharing

OPT Lesson_04_Theory_04_GeneralizedMean https://drive.google.com/file/d/1nO_ama3jrWlLfQ6SgqGfoEpLBXBSZ16L/view?usp=sharing

OPT Lesson_04_Theory_05_ArithmeticMean https://drive.google.com/file/d/1iCweHFvSi9yIt_JWxO_Fz1h5shvOrAxf/view?usp=sharing

OPT Lesson_04_Theory_06_Median https://drive.google.com/file/d/1aF13Houc7svk0bh9jnVqDXiRU0MoFM9n/view?usp=sharing

OPT Lesson_04_Theory_07_Mode https://drive.google.com/file/d/13dwz6P-HNTZxR_OsfMLk-AV1_bP6-Ijr/view?usp=sharing

OPT Lesson_04_Theory_08_NaiveCovariance_Variance https://drive.google.com/file/d/10_lDzwO5BjUlA--rVPvvc_Wo8k_DFAz5/view?usp=sharing

Lesson_04_Theory_09_QuickIntroLinearRegression https://drive.google.com/file/d/1qiJ8l7TgiSuyh3omiK031tH0QPasxv0u/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

Lesson_04_Apps_01_WorldWindowToDeviceVieportTransform https://drive.google.com/file/d/1jB602QC-CfCaZcMrNR793YWrZX2krYWR/view?usp=sharing

Lesson_04_Apps_02_Transform_ManualMethodExample https://drive.google.com/file/d/1U24jxMgfAhmDv8yoDIWMR0ErR4WX4Zf3/view?usp=sharing

Lesson_04_Apps_03_InteractiveDeviceViewport https://drive.google.com/file/d/1UiSnUoZzwftjxmxynBq8QkLlZZr8hX0B/view?usp=sharing

OPT Lesson_04_Apps_04_InteractiveWorldWindow https://drive.google.com/file/d/1cZe_SsBeEB5G9osrz9v3obzJjIc7p_tu/view?usp=sharing

OPT Lesson_04_Apps_05_TransformMatrix_GraphicsTransform https://drive.google.com/file/d/1MF1gZgR3WDWaC1FS3W7qMXWZP1fEexgR/view?usp=sharing

OPT Lesson_04_Apps_06_WordCloudExample https://drive.google.com/file/d/1aJjume4UrVqfbrmAuqEdapnYcmhLgM4I/view?usp=sharing

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 4 Nov 2020, or -1 penalty on final grade may apply ]

Researches about theory (R)

10_R. Explain a unified conceptual framework to obtain all most common measures of central tendency using the concept of distance (or "premetric" in general).

11_R. What are the most common types of means known? Find one example where these two types of means arise naturally: geometric, harmonic.

12_R. Explain the idea underlying the measures of dispersion and the reasons of their importance.

13_R. Find out all the most important properties of the linear regression.

Applications / Practice (A) [work on this at least 30' a day, all days]

9_A. Prepare separately the following charts: 1) Scatterplot, 2) Histogram/Column chart [in the histogram, within each class interval, draw also a vertical colored line where lies the true mean of the observations falling in that class] and 3) Contingency table, using the graphics object and the Drawstring(), MeasureString(), DrawLine(), etc. methods.When done, merge these charts in your previous application 7_A. Use them to represent 2 numerical variables that you select from a CSV file. In particular, in the same picture box, you will make 2 separate charts: 1 rectangle (chart) will contain the contingency table, and 1 rectangle (chart) will contain the scatterplot, with the histograms/column charts and rug plots drawn respectively near the two axis (and oriented accordingly).

OPT 10_A. Implement your own algorithm to compute a frequency distribution of the words from any text (possibly judiciously scraped from websites) and draw some personal graphical representation of the "word cloud".

Researches about applications (RA)

7_RA. Do a research about the real world window to viewport transformation.

OPT 8_RA. Do a research with examples about how matrices and homogeneous coordinates can be useful for graphics transformations and charts.

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on statistical theory:

Summary stats https://en.wikipedia.org/wiki/Summary_statistics , https://statistics.laerd.com/statistical-guides/measures-central-tendency-mean-mode-median.php#:~:text=A%20measure%20of%20central%20tendency,also%20classed%20as%20summary%20statistics . , https://math.stackexchange.com/questions/2554243/understanding-the-mean-minimizes-the-mean-squared-error , https://stats.stackexchange.com/questions/200282/explaining-mean-median-mode-in-laymans-terms , http://dida.fauser.edu/calcolo/calcol3/valmedi.htm#:~:text=Una%20propriet%C3%A0%20caratteristica%20della%20mediana,scarti%20da%20qualunque%20altro%20valore

Dimensional analysis: https://en.wikipedia.org/wiki/Dimensional_analysis

Metrics: https://en.wikipedia.org/wiki/Metric_(mathematics) https://en.wikipedia.org/wiki/Metric_(mathematics)#Premetrics
Central tendency https://en.wikipedia.org/wiki/Central_tendency#Solutions_to_variational_problems

Discrete distance https://en.wikipedia.org/wiki/Discrete_space

Dispersion https://statistics.laerd.com/statistical-guides/measures-of-spread-range-quartiles.php

Variance https://en.wikipedia.org/wiki/Variance , https://stats.stackexchange.com/questions/239379/what-is-the-difference-between-mean-squared-deviation-and-variance , https://en.wikipedia.org/wiki/Squared_deviations_from_the_mean , https://math.stackexchange.com/questions/711135/derivation-of-runningonline-variances-formula

Variance algos https://it.wikipedia.org/wiki/Algoritmi_per_il_calcolo_della_varianza

For applications

Running Mean and Variance https://math.stackexchange.com/questions/20593/calculate-variance-from-a-stream-of-sample-values , https://www.johndcook.com/blog/standard_deviation/

Transforms http://math.hws.edu/graphicsbook/c2/s3.html , https://en.wikipedia.org/wiki/Transformation_matrix#/media/File:2D_affine_transformation_matrix.svg

Matrices https://docs.microsoft.com/en-us/dotnet/desktop/winforms/advanced/why-transformation-order-is-significant?view=netframeworkdesktop-4.8

http://csharphelper.com/blog/2015/12/draw-round-circles-in-a-scaled-coordinate-system-in-c/

Web scraping https://en.wikipedia.org/wiki/Web_scraping (a stop words list: http://snowball.tartarus.org/algorithms/italian/stop.txt )

_______________________________________________________________________________________

- LESSON 05 - [05 Nov 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, " OPT" denotes homework that can be skipped.

Theory

OPT Lesson_05_Theory_01_VarianceDecomposition_CoefficientOfDetermination https://drive.google.com/file/d/1beOMXQbzW_f99vaEMQWU81qvN9XeWGwa/view?usp=sharing

Lesson_05_Theory_02_MeasureTheory_ProbabilityAxioms https://drive.google.com/file/d/1MmJoRZKqXibg7vA3z7QWkmAUbBB7HVv7/view?usp=sharing

Lesson_05_Theory_03_ParametricInference_InductiveReasoning https://drive.google.com/file/d/1yR3Rr4an2eQpCVFyxm91M_DYzgfSyAAu/view?usp=sharing

Lesson_05_Theory_04_RoleOfProbabilityInStatistics https://drive.google.com/file/d/1DOyD8x4O2llZc_NqhGtFFEKrCPKMRTGV/view?usp=sharing

Lesson_05_Theory_05_ProbabilitySpaceAndStatistics_RandomVariables https://drive.google.com/file/d/1eQLx-K8chF3Mdrwu0mSTkl7wrQ7cT94S/view?usp=sharing

Lesson_05_Theory_06_QuickIntroToLebesgueIntegralAndMeanVarianceOfRandomVariables https://drive.google.com/file/d/1AhsZ6prIqAHu06fx1l2Cxokq60EnQ7g_/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

(revise your stat application)

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 11 Nov 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

14_R. Think and explain in your own words what is the role that probability plays in Statistics and the relation between "empirical" objects - such as the observed distribution and frequencies etc - and "theoretical" counterparts.

15_R. Explain how parametric inference works and the main ideas of statistical induction, including the role of Bayes theorem and the different approach between "bayesian" and "frequentist".

16_R. Do some practical examples where you explain how the elements of an abstract probability space relates to more concrete concepts when doing statistics.

Applications / Practice (A) [work on this at least 30' a day, all days]

11_A. Make a short demonstrative program where you apply both the Riemann and Lebesgue approach to integration to compute numerically (with an increasingly large number of subdivisions) the integral on a bounded continuous function of your choice and compare the results. [Optionally, show with an animation, using the graphics object, the convergence to a limit, as the number of subdivisions of the function domain (for Riemann) or range (for Lebesgue) increases.]

OPT 12_A. Add regression lines to your revised statistical application (parser + statistical/charting engine).

Researches about applications (RA)

9_RA. Do a research about the various methods to generate, from a Uniform([0,1)), all the most important random variables (discrete and continuous). [Wherever found, save snippets of code of such algorithms, as they will be useful for the final exam and next homeworks.] https://en.wikipedia.org/wiki/List_of_probability_distributions

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Variance Decomposition https://murraylax.org/rtutorials/regression_anovatable.pdf
Coefficient of Determination https://en.wikipedia.org/wiki/Coefficient_of_determination
Correlation coefficient https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
Cauchy Schwarz https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality

videos:

https://www.youtube.com/watch?v=ZJsOOCghQJ0 "Cumulative Distribution Function (1 of 3: Definition)"

Lebesgue Stielties integral https://en.wikipedia.org/wiki/Lebesgue_integration , https://en.wikipedia.org/wiki/Lebesgue%E2%80%93Stieltjes_integration , https://matheducators.stackexchange.com/questions/5981/what-is-a-good-way-to-explain-the-lebesgue-integral-to-non-math-majors , https://www.whitman.edu/Documents/Academics/Mathematics/2017/Wang.pdf , http://www.math.nagoya-u.ac.jp/~richard/teaching/s2017/Nelson_2015.pdf , https://math.stackexchange.com/questions/1267330/on-the-horizontal-integration-of-the-lebesgue-integral
Fubini-Tonelli https://en.wikipedia.org/wiki/Fubini%27s_theorem
Layer cake representation https://en.wikipedia.org/wiki/Layer_cake_representation , https://math.stackexchange.com/questions/998633/how-is-fubinis-theorem-used-in-the-following-proof , https://math.stackexchange.com/questions/338275/proof-of-int-0-inftyptp-1-mu-xfx-geq-t-d-mut-int-0-inft
Simple function https://math.stackexchange.com/questions/2481592/step-function-vs-simple-function

Dirichlet https://en.wikipedia.org/wiki/Nowhere_continuous_function

Random Variables, generation https://www.cse.wustl.edu/~jain/books/ftp/ch5f_slides.pdf , https://encyclopediaofmath.org/wiki/Generating_random_variables , https://web.mit.edu/urban_or_book/www/book/chapter7/7.1.3.html , https://towardsdatascience.com/how-to-generate-random-variables-from-scratch-no-library-used-4b71eb3c8dc7 , http://www.columbia.edu/~mh2078/MonteCarlo/MCS_Generate_RVars.pdf , http://www.stat.tamu.edu/~jnewton/604/chap3.pdf
Inverse transform sampling https://en.wikipedia.org/wiki/Inverse_transform_sampling
Rejection sampling https://en.wikipedia.org/wiki/Rejection_sampling
Ziggurat algo https://en.wikipedia.org/wiki/Ziggurat_algorithm , http://www.jstatsoft.org/v05/i08/paper , https://core.ac.uk/download/pdf/6287927.pdf
Box Muller transform https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform
Other normal http://home.iitk.ac.in/~kundu/paper104.pdf
Monte Carlo methods https://en.wikipedia.org/wiki/Monte_Carlo_method

For applications

Definite integral video https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-3/v/riemann-sums-and-integrals , https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new/ab-6-3/a/definite-integral-as-the-limit-of-a-riemann-sum
https://mathinsight.org/calculating_area_under_curve_riemann_sums
https://www.emathhelp.net/calculators/calculus-2/riemann-sum-calculator/
https://en.wikipedia.org/wiki/Riemann_sum
https://www.desmos.com/calculator/tgyr42ezjq?lang=it

Running Regression https://www.johndcook.com/blog/running_regression/
One pass skeweness and kurtosis https://www.johndcook.com/blog/skewness_kurtosis/

_______________________________________________________________________________________

- LESSON 06 - [12 Nov 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, " OPT" denotes homework that can be skipped.

Theory

Lesson_06_Theory_01_RecapAndProbabilityDistribution https://drive.google.com/file/d/1_mIeSn8vJBh3u82JyjZmzVAi34EATop9/view?usp=sharing

Lesson_06_Theory_02_SequencesOfRandomVariables_ConvergenceInDistribution https://drive.google.com/file/d/1SZZflBa6ek20bxZeFAqph1JYg3hKbtHX/view?usp=sharing

Lesson_06_Theory_03_ConvergenceInProbabilityAndQuickIntroToLLN https://drive.google.com/file/d/1tbRiLN6w2RGg172IbcEdUzDsHOqX2Bj4/view?usp=sharing

OPT (some additional explanation for exercise 13_A) Lesson_06_Theory_04_ExerciseOnLLN https://drive.google.com/file/d/1etyfP_jm5N3p8aX1qmjbLmJUVs7b9STT/view?usp=sharing

Lesson_06_Theory_05_MeanVarianceOfSampleMean https://drive.google.com/file/d/1XBSvmDylVTNpo_RG8vwuE8ouizRM1gCs/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

(revise and refine your stat application)

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 18 Nov 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

17_R. Exercise 13_A is remarkably useful from a didactical point of view for several reasons, including:

1) illustrates with visual evidence the law of large numbers LLN, and the various definitions of convergence
2) illustrates the binomial distribution
3) illustrates the convergence of the binomial to the normal
4) illustrates the central limit theorem [in anticipation of a topic we will study later]
5) provides a basic example of stochastic process (sequence of r.v.'s defined on the same probability space) [in anticipation of a topic we will study later]

For each of the above 5 points, research on the web (stackexchange, wiki, etc.) and explain what each point is about. For each point, do your personal considerations about what your simulation is suggesting you.

Applications / Practice (A) [work on this at least 30' a day, all days]

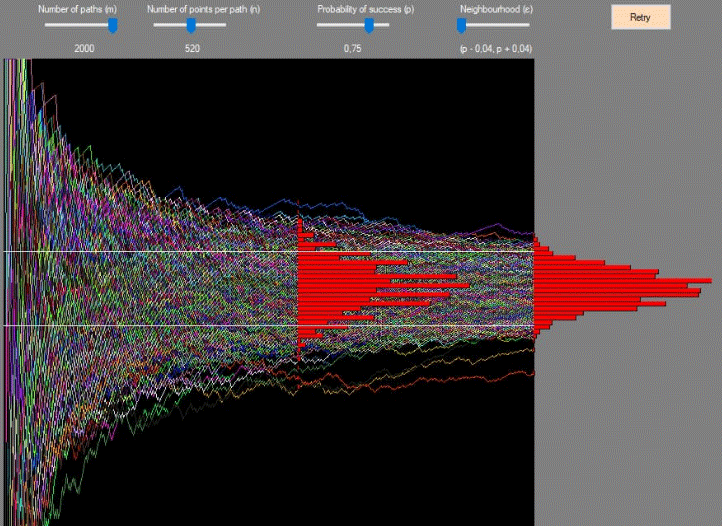
13_A. Exercise described in video (Theory_04). Summary:

Generate and represent m paths of n point each (m, n are program parameters), where each point represents a pair of: time index and relative frequency of success (i, f(i)), where f(i) is the sum of i Bernoulli random variables p^x(1-p)^(1-x) observed at the times j=1, ..., i.
At time n (last time) and one other chosen inner time 1<j<n (j is a program parameter) create and represent with histogram the distribution of f(i).
At the same times (j and n), compute the absolute and relative frequency of the f(i)'s contained in the interval (p-ε, p+ε), where ε is a program parameter.

Empirical Freqency Sample Paths (source: homework screenshot by Lorenzo Zara )

(The general scheme of this exercise, will also be "reused" in next homeworks where we will consider other, more interesting, stochastic processes.)

OPT 14_A. Add total variance decomposition and computation of the coefficient of determination (make sure all your computations are done with online algorithms (e.g. with online algorithms (e.g. https://www.johndcook.com/blog/running_regression// etc.).

Researches about applications (RA)

10_RA. Do a research about the various methods proposed to compute the running median (one pass, online algorithms). Store (cite sources) the algorithm that you think is a good candidate, explaining briefly how it works and possibly show a quick demo.

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Probability distribution https://en.wikipedia.org/wiki/Probability_distribution , https://stats.stackexchange.com/questions/489948/difference-between-uniform-laws-of-large-numbers-and-law-of-large-numbers?rq=1 , https://en.wikipedia.org/wiki/Probability_mass_function , https://en.wikipedia.org/wiki/Probability_density_function , https://en.wikipedia.org/wiki/Cumulative_distribution_function

Convergence https://www.youtube.com/watch?v=l_YZ096WH74 , https://www.youtube.com/watch?v=ZKqzA81Nz2Y https://stats.stackexchange.com/questions/2230/convergence-in-probability-vs-almost-sure-convergence , https://math.stackexchange.com/questions/3776889/interpreting-almost-sure-convergence , https://stats.stackexchange.com/questions/141219/almost-sure-convergence-does-not-imply-complete-convergence, https://math.stackexchange.com/questions/2926296/weak-convergence-of-measures-implying-almost-sure-convergence-of-random-variable

Variance of relative frequency https://math.stackexchange.com/questions/1526230/variance-of-relative-frequency#:~:text=If%20we%20perform%2010%20trials,1%E2%88%92p)%2F10.

LLN https://en.wikipedia.org/wiki/Law_of_large_numbers , https://stats.stackexchange.com/questions/47310/weak-law-of-large-numbers-redundant , https://stats.stackexchange.com/questions/22557/central-limit-theorem-versus-law-of-large-numbers , https://stats.stackexchange.com/questions/45695/conditions-in-law-of-large-numbers?rq=1 , https://stats.stackexchange.com/questions/29882/when-does-the-law-of-large-numbers-fail?rq=1 , https://stats.stackexchange.com/questions/24562/why-law-of-large-numbers-does-not-apply-in-the-case-of-apple-share-price?rq=1

For applications

Median https://stats.stackexchange.com/questions/134/algorithms-to-compute-the-running-median , http://www.dsalgo.com/2013/02/RunningMedian.php.htmll , https://www.cs.cornell.edu/courses/cs2110/2009su/Lectures/examples/MedianFinding.pdf , https://github.com/GuyKomari/Median-Online-Algorithm

_______________________________________________________________________________________

- LESSON 07 - [19 Nov 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT" denotes homework that can be skipped.

Theory

Lesson_07_Theory_01_ConcentrationInequalities_Markov https://drive.google.com/file/d/1gnXs8gwUEt5GgNoxmjpFENY7w8SQHcx1/view?usp=sharing

Lesson_07_Theory_02_ConcentrationInequalities_Chebyshev_LLNProof https://drive.google.com/file/d/1QtYA2hgZLaaA3hZg_VL8Pl-U84MqK-CX/view?usp=sharing

OPT Lesson_07_Theory_03_AlmostSureConvergence_BorelCantelli https://drive.google.com/file/d/1Db4wEwHhgMae2BPJ5f049xLFNh2YLHkk/view?usp=sharing

Lesson_07_Theory_04_GlivenkoCantelli_UniformConvergenceOfEmpiricalCDF https://drive.google.com/file/d/1yIEmHhqe0h1i-nBg_vCcJ0yzSAjfav6a/view?usp=sharing

Lesson_07_Theory_05_Standardization_QuickIntroToCLT https://drive.google.com/file/d/1Oosog1d1O461OlK4mOwTisrUmR_HqrEs/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

(revise and refine 1) your stat application and 2) your stochastic process simulator)

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 25 Nov 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

18_R. History and derivation of the normal distribution. Touch, at least, the following three perspectives, putting them into an historical context to understand how the idea developed and trying to understand the different derivations:

1) as approximation of binomial (De Moivre)
2) as error curve (Gauss)
3) as limit of sum of independent r.v.'s (Laplace)

some video sources:

"The Evolution of the Normal Distribution" https://www.maa.org/sites/default/files/pdf/upload_library/22/Allendoerfer/stahl96.pdf
"The Normal Distribution: A derivation from basic principles" https://www.alternatievewiskunde.nl/QED/normal.pdf
"A Derivation of the Normal Distribution" https://web.sonoma.edu/users/w/wilsonst/papers/Normal/default.html
https://math.stackexchange.com/questions/384893/how-was-the-normal-distribution-derived
"Normal Distributions: The History of the Discovery of Normal Distributions" https://www.youtube.com/watch?v=BXof869EC68
"Normal Distribution Example and History Part 1" https://www.youtube.com/watch?v=XUT5Oadidbw
"History of the Normal Distribution" https://www.youtube.com/watch?v=-ftS9UqdA-g
"Normal Distribution, Why is it "Normal"? " https://www.youtube.com/watch?v=nyibbuGFsr8
"Normal distribution's probability density function derived in 5min" https://www.youtube.com/watch?v=ebewBjZmZTw
"The Normal Distribution (1 of 3: Introductory definition)" https://www.youtube.com/watch?v=mHTp7azBhGs
etc.

Applications / Practice (A) [work on this at least 30' a day, all days]

15_A. Simple illustration of the Glivenko-Cantelli theorem ( http://home.uchicago.edu/~amshaikh/webfiles/glivenko-cantelli_topics.pdf ).
Consider random variables from a Uniform distribution (not necessarily in the same range), and create both the histogram and the empirical CDF of the sample mean. Show with an animation what happens when the number of observations increases. What do we see here?
(This exercise can be best and more easily done by using the scheme of previous homework 13_A, simply using the empirical mean in place of the empirical frequency, and, on the right, drawing the empirical CDF vertically, along with the histogram).

PlotEmpiricalCdfAndCompareWithSamplingDistributionExample_01

(source: https://it.mathworks.com/help/stats/cdfplot.html )

OPT 16_A. Simple variation of your application to simulate stochastic processes.
Add to your previous program 13_A the following.
Same scheme as previous program, except changing the way to compute the values at each time. Starting from value 0 at time 0, at each new time compute Y(i) = Y(i-1) + Random step(i). Where Random step(i) is a Rademacher random variable ( https://en.wikipedia.org/wiki/Rademacher_distribution ).
At time n (last time) and one other chosen inner time 1<j<n (j is a program parameter) create and represent with histogram the distribution of Y(i).

(source: https://www.datatime.eu/public/StatApp2020/ )

OPT 17_A. "Add on" for your stat application.
Add second order regression to your statistical application (where possible, always use "on line" algorithms for the various computations):
https://www.azdhs.gov/documents/preparedness/state-laboratory/lab-licensure-certification/technical-resources/calibration-training/12-quadratic-least-squares-regression-calib.pdf
https://math.stackexchange.com/questions/267865/equations-for-quadratic-regression

second order regression (source: https://journals.plos.org/plosone/article/figure?id=10.1371/journal.pone.0140423.g005 )

Researches about applications (RA)

11_RA Do a research about the random walk and its properties. Looking at your possible simulation in exercise 15_A, how would you describe the beaviour of the distribution of Y, as n increases ? What are mean and variance of Y at step n ?

https://stats.stackexchange.com/questions/159650/why-does-the-variance-of-the-random-walk-increaseasese

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Probability: Theory and Examples, Rick Durrett https://services.math.duke.edu/~rtd/PTE/PTE5_011119.pdf
MIT Fundamentals of Probability https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-436j-fundamentals-of-probability-fall-2018/lecture-notes/MIT6_436JF18_lec04.pdf

Markov inequality https://en.wikipedia.org/wiki/Markov%27s_inequalityy
Chebyshev inequality https://en.wikipedia.org/wiki/Chebyshev%27s_inequality
"Weak Law of Large Numbers" from MIT https://www.youtube.com/watch?v=3eiio3Tw7UQ
Borel Cantelli https://en.wikipedia.org/wiki/Borel%E2%80%93Cantelli_lemma , https://stats.stackexchange.com/questions/486885/converge-of-scaled-bernoulli-random-process
Simplest proof of strong LLN https://math.stackexchange.com/questions/3068125/proofing-the-strong-law-of-large-numbers
https://math.stackexchange.com/questions/406226/central-limit-theorem-implies-law-of-large-numbers?rq=1
Infinite Monkey https://en.wikipedia.org/wiki/Infinite_monkey_theorem

Glivenko-Cantelli Theorem https://mathigon.org/course/intro-statistics/empirical-cdf-convergence , https://www.stat.berkeley.edu/~bartlett/courses/2013spring-stat210b/notes/8notes.pdf , http://users.stat.umn.edu/~helwig/notes/den-Notes.pdf

For applications

Random Walk https://en.wikipedia.org/wiki/Random_walk , http://www.math.caltech.edu/~2016-17/2term/ma003/Notes/Lecture16.pdf
https://en.wikipedia.org/wiki/Rademacher_distribution

_______________________________________________________________________________________

- LESSON 08 - [26 Nov 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT " denotes homework that can be skipped.

Theory

"OPT" Lesson_08_Theory_01_AlmostSurely_ProbabilityZero https://drive.google.com/file/d/1WTh5uDhPCBHJOGiWrlCu-Zk1_F74W1r5/view?usp=sharing

Lesson_08_Theory_02_OrderStatistics https://drive.google.com/file/d/1M_llkCcuDl1sAx7EMgwVW7JkRO5HegIc/view?usp=sharing

Lesson_08_Theory_03_Quantiles https://drive.google.com/file/d/1ZvhQsMh7fRKUchi9-7aTAQuNxCnf9Fb9/view?usp=sharing

Lesson_08_Theory_04_QuantileFunction_GeneralizedInverse https://drive.google.com/file/d/1nzQjbU9l-parcpgGcP6yJ1mAIh_cDsiM/view?usp=sharing

Lesson_08_Theory_05_OrderStatistics_Density https://drive.google.com/file/d/1jaxaDQRvuxvAdHkF-18lxx0Zn8Xz8KX_/view?usp=sharing

Lesson_08_Theory_06_OrderStatistics_CDF https://drive.google.com/file/d/191v43xoMG5q05oAqamkwNXNEgVQm9fbH/view?usp=sharing

Lesson_08_Theory_07_Ranks https://drive.google.com/file/d/1U4v5nf1cGBFjjQhy8_5BcPj9CmL3J5a6/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

[revise and refine 1) your stat application, adding the quartiles and 2) your stochastic process simulator, adding the new process indicated in 18_A]

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 2 Dec 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

19_R. Distributions of the order statistics: look on the web for the most simple (but still rigorous) and clear derivations of the distributions, explaining in your own words the methods used.

20_R. General correlation coefficient for ranks and the most common indices that can be derived by it. Can you make some interesting example of computation of these correlation coefficients for for ranks?

Applications / Practice (A) [work on this at least 30' a day, all days]

18_A. Discover a new important process by yourself !

Consider the general scheme we have used so far to simulate some stochastic processes (such as the relative frequency of success in a sequence of trials, the sample mean and the random walk) and now add this new process to our simulator.
Same scheme as previous program (random walk), except changing the way to compute the values of the paths at each time. Starting from value 0 at time 0, for each of m paths, at each new time compute P(i) = P(i-1) + Random step(i), for i = 1, ..., n, where Random step(i) is now a Bernoulli random variable with success probability equal to λ * (1/n) (where λ is a user parameter, eg. 50, 100, ...).
At time n (last time) and one (or more) other chosen inner time 1<j<n (j is a program parameter) create and represent with histogram the distribution of P(i).

Represent also the distributions of the following quantities (and any other quantity that you think of interest):
- Distance (time elapsed) of individual jumps from the origin
- Distance (time elapsed) between consecutive jumps

19_A. Add to your statistical application, on each variable histogram, and across the scatterplot, 3 lines indicating the 3 quartiles (use online algos for computations).

Researches about applications (RA)

12_RA. Find out what you have just generated in exercise 18_A. How can you interpret what you see? Can you find out about all the well known distributions that "naturally (and "magically") arise" in this process ?

Hints:
https://www.probabilitycourse.com/chapter11/11_1_2_basic_concepts_of_the_poisson_process.php
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-262-discrete-stochastic-processes-spring-2011/course-notes/MIT6_262S11_chap02.pdf
https://towardsdatascience.com/the-poisson-distribution-and-poisson-process-explained-4e2cb17d459

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Almost surely https://en.wikipedia.org/wiki/Almost_surely

General correlation coefficient https://en.wikipedia.org/wiki/Rank_correlation
Ranking https://en.wikipedia.org/wiki/Ranking#Ranking_in_statistics
https://us.humankinetics.com/blogs/excerpt/what-is-rank-order-correlation

videos:
https://www.youtube.com/watch?v=DE58QuNKA-c ("How To... Calculate Spearman's Rank Correlation Coefficient (By Hand)")
https://www.youtube.com/watch?v=gDNmhEBZAO8 ("Rank Correlations: Spearman's and Kendall's Tau")

Quantile function

Quantile function https://en.wikipedia.org/wiki/Quantile_function
Generalized Inverse https://math.stackexchange.com/questions/1801362/generalized-inverse-of-a-function
https://math.stackexchange.com/questions/210683/proof-that-quantile-function-characterizes-probability-distribution
https://math.stackexchange.com/questions/3378799/is-the-sample-quantile-unbiased-for-the-true-quantile

videos
https://www.youtube.com/watch?v=ASHPdWCPBXE ("Cumulative Distribution Function (3 of 3: Locating quantiles)")

For applications

https://stats.stackexchange.com/questions/325539/lambda-exponential-vs-poisson-interpretation/325662
http://www.it.uu.se/edu/course/homepage/fussmobb/ht06/computing/labb5.pdf
http://www.math.unl.edu/~sdunbar1/ProbabilityTheory/Lessons/Poisson/PoissonOld/poisson.shtml
Jump process https://en.wikipedia.org/wiki/Jump_process

_______________________________________________________________________________________

- LESSON 09 - [03 Dic 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT " denotes homework that can be skipped.

Theory

Computer applications, and language fundamentals for statistical algos

[revise and refine 1) your stat application, as indicated in 21_A, 2) your stochastic process simulator, as indicated in 20_A]

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 9 Dec 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

21_R.What is a Brownian diffusion process. History, importance, definition and applications.

22_R.An "analog" of the CLT for stochastic process: the Brownian motion as limit of random walk and the functional CLT (Donsker theorem). Explain the intuitive meaning of this result.

Applications / Practice (A) [work on this at least 30' a day, all days]

20_A. Discover "the" fundamental stochastic process by yourself !

Consider the general scheme we have used so far to simulate some stochastic processes (such as the relative frequency of success in a sequence of trials, the sample mean, the random walk, the Poisson point process) and now add this new process to our simulator.
Same scheme as previous simulations programs, except changing the way to compute the values of the paths at each time. Starting from value 0 at time 0, for each of m paths, at each new time compute P(t) = P(t-1) + Random step(t), for t = 1, ..., n, where Random step(t) is now: σ * sqrt(1/n) * Z(t), where Z(t) is a N(0,1) random variable (the deviation σ is a user parameter, to scale the process dispersion).
At time n (last time) and one (or more) other chosen inner time 1<j<n (j is a program parameter) create and represent with histogram the distribution of P(t). Observe the behavior of the process for large n.

21_A. Refine your statistical application in the following way:

To the contingency table, add or make sure it has the following features: 2) the option to display the frequencies either in absolute or relative form, with totals 2) the option to display the histograms "around" the table, in a compact form.

Researches about applications (RA)

13_RA. Find out what you have just generated in exercise 20_A.

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Stochastic Process definition http://stat.math.uregina.ca/~kozdron/Teaching/Regina/862Winter06/Handouts/revised_lecture1.pdf , https://www.kent.ac.uk/smsas/personal/lb209/files/notes1.pdf

Prof. Steve Lalley course page https://galton.uchicago.edu/~lalley/Courses/ http://galton.uchicago.edu/~lalley/Courses/385/index.html

Set, collection, class, family, sequence difference https://math.stackexchange.com/questions/223405/can-elements-in-a-set-be-duplicated , https://stackoverflow.com/questions/821079/when-to-use-set-vs-collection#:~:text=The%20practical%20difference%20is%20that,unordered%2C%20while%20Collection%20does%20not . , https://en.wikipedia.org/wiki/Partially_ordered_set , https://www.samuel-drapeau.info/math/2015/10/04/family-vs-collection/#:~:text=Given%20a%20set%20X%2C%20a,of%20elements%20is%20not%20possible . , https://en.wikipedia.org/wiki/Subset , https://www.stat.auckland.ac.nz/~fewster/325/notes/ch1annotated.pdf , https://math.stackexchange.com/questions/604305/what-is-difference-between-stochastic-process-and-a-sequence-of-random-variables , https://math.stackexchange.com/questions/1593384/what-is-the-difference-between-an-indexed-family-and-a-sequence/1593393#:~:text=Formally%2C%20this%20sequence%20is%20a,I%20can%20be%20any%20set.&text=Here%20you%20can%20see%20that,the%20set%20of%20positive%20integers . , https://mathworld.wolfram.com/Collection.html , https://math.stackexchange.com/questions/1601545/whats-the-definition-of-a-collection , https://math.stackexchange.com/questions/172966/what-are-the-differences-between-class-set-family-and-collection . https://en.wikipedia.org/wiki/Function_(mathematics ) , https://en.wikipedia.org/wiki/Binary_relation , https://en.wikipedia.org/wiki/Cartesian_product

Discrete and continuous time https://en.wikipedia.org/wiki/Discrete_time_and_continuous_time
Discrete and continuous state space https://www.researchgate.net/figure/Discrete-vs-continuous-time-and-discrete-vs-continuous-state-space-models_fig1_220053939 https://en.wikipedia.org/wiki/Stochastic_process

Stationary Independent Increments https://stats.stackexchange.com/questions/476740/what-is-a-random-process-with-stationary-independent-increments
Independent increments of Poisson process https://stats.stackexchange.com/questions/69498/how-to-prove-the-independent-and-stationary-increment-of-a-poisson-process

Videos:

https://www.youtube.com/watch?v=7mmeksMiXp4 "Brownian motion #1 (basic properties)
https://www.youtube.com/watch?v=PPl-7_RL0Ko "17. Stochastic Processes II"

For applications

Simulating Brownian motion (BM) and geometric Brownian motion (GBM) http://www.columbia.edu/~ks20/4404-Sigman/4404-Notes-sim-BM.pdf

_______________________________________________________________________________________

- LESSON 10 - [10 Dic 2020]

STREAMING or VIDEOS LESSONS:

Note: "OPT" indicates optional video material for extra help: it can be skipped. Same for homework, "OPT " denotes homework that can be skipped.

Theory

Lesson_10_Theory_01_QuickIntroToSDE https://drive.google.com/file/d/1maWgfMHjUMtoK2aAORZHsoHE5ix4SKWy/view?usp=sharing

Lesson_10_Theory_02_GeometricBrownianMotionSDE https://drive.google.com/file/d/1dNFgsipYz9KVhHs7h7zUk_WDwIPWSoWC/view?usp=sharing

Lesson_10_Theory_03_QuickIntroToSolutionOfSDE_1 https://drive.google.com/file/d/1cY6VCO-7-s8xieKRh_OA0-Ven_fOclG9/view?usp=sharing

Lesson_10_Theory_04_QuickIntroToSolutionOfSDE_2 https://drive.google.com/file/d/1whpVDpOYSYypoGGki_3BxHbN-bF3TQ1s/view?usp=sharing

Lesson_10_Theory_05_SolutionForStandardBrownianMotion https://drive.google.com/file/d/1nlMSkhVJmvW41W4RshQi8sXHs696Cu5c/view?usp=sharing

Lesson_10_Theory_06_SolutionForGeneralBrownianMotion https://drive.google.com/file/d/1WjZ_64zT2EyScoQkWZIsQfufSyjEtful/view?usp=sharing

Lesson_10_Theory_07_Ornstein_Uhlenbeck_VasicekSDE https://drive.google.com/file/d/1bLByibiq20gza6WFNqygSHo0QiB3g4nh/view?usp=sharing

Lesson_10_Theory_08_Euler_Maruyama_Method https://drive.google.com/file/d/1XJkfymX26o_yK7AdVaGnS15q5RSdFSY0/view?usp=sharing

Computer applications, and language fundamentals for statistical algos

[revise and refine 1) your stat application and 2) your stochastic process simulator, adding the processes as indicated in 22_A, 23_A]

HOMEWORK / ASSIGNMENTS (to be published by the student on the personal blog) : [DATE DUE: send your link within 16 Dec 2020, or -1 on final grade penalty may apply]

Researches about theory (R)

23_R. The Geometric Brownian motion and its importance for applications. The Ornstein-Uhlenbeck / Vasicek models and the concept of mean reversion.

24_R. Stochastic differential equations (SDE). What are the differences respect to the ordinary differential equations (ODE). Try to understand and explain in your own words why the Itô calculus has been introduced and what is the main intuition behind the Itô integral.

Applications / Practice (A) [work on this at least 30' a day, all days]

22_A. Add to your simulation program, the simulation of the SDE for Geometric Brownian motion and Vasicek process.

23_A. Refine your statistical application and your simulation station in the following way. Do a complete test, both "smart monkey" and "dumb monkey", ( https://en.wikipedia.org/wiki/Monkey_testing ), fixing all issues and making all the desired final refinements to your 2 main applications developed during the course.

Researches about applications (RA)

14_RA.SDE and methods for numerical solution.

REFERENCES / SOURCES / USEFUL LINKS:

Additional useful readings on theory:

Sampling from SDE https://quant.stackexchange.com/questions/54266/sampling-from-sde

Brownian motion http://www.math.unl.edu/~sdunbar1/MathematicalFinance/Lessons/StochasticCalculus/GeometricBrownianMotion/geometricbrownian.pdf , http://www-users.math.umn.edu/~grayx004/pdf/FM5002/BMandGBMdoc.pdf

Vasicek https://en.wikipedia.org/wiki/Vasicek_model
Ornstein–Uhlenbeck process https://en.wikipedia.org/wiki/Ornstein%E2%80%93Uhlenbeck_process

Stochastic Differential Equation solution for Geometric Brownian Motion https://math.stackexchange.com/questions/2288421/stochastic-differential-equation-solution-for-geometric-brownian-motion

Itô calculus https://en.wikipedia.org/wiki/It%C3%B4_calculus , https://quant.stackexchange.com/questions/23158/ito-formula-for-stochastic-integral

Videos:

https://www.youtube.com/watch?v=p_di4Zn4wz4 ["Differential equations, studying the unsolvable"]

https://www.youtube.com/watch?v=AShtIGjHOTQ ["Arithmetic Brownian motion: solution ..."]
https://www.youtube.com/watch?v=qdbkvD4N-us [" 21. Stochastic Differential Equations "]

https://www.youtube.com/watch?v=Z5yRMMVUC5w ["18. Itō Calculus"]

For applications and exam

Euler–Maruyama method https://en.wikipedia.org/wiki/Euler%E2%80%93Maruyama_method , https://www.math.kit.edu/ianm3/lehre/nummathfin2012w/media/euler_maruyama.pdf
Numerical Simulation of SDE's https://epubs.siam.org/doi/pdf/10.1137/S0036144500378302
Basic affine jump diffusion https://en.wikipedia.org/wiki/Basic_affine_jump_diffusion
Compound Poisson process https://en.wikipedia.org/wiki/Compound_Poisson_process
"Merton’s Jump-Diffusion Model" https://www.csie.ntu.edu.tw/~lyuu/finance1/2015/20150513.pdf
Cox–Ingersoll–Ross model https://en.wikipedia.org/wiki/Cox%E2%80%93Ingersoll%E2%80%93Ross_modell
Heston model https://en.wikipedia.org/wiki/Heston_model
Hull–White model https://en.wikipedia.org/wiki/Hull%E2%80%93White_model

- LESSON 11 - [17 Dic 2020]

[Skipped on students' request, to allow preparation for exam and completion of projects]

_____________________________________________________________________________________

Final exam instructions:

1) Make sure you book the exam on Infostud
2) Send the Projects for the "written" exam

Final projects for exam (2 applications delivered).

Project 1) Refine completely your statistical application, by enclosing all the features we have discussed during the course (even those marked as "optional" in the homeworks).

Project 2) Add a jump diffusion process to your Euler-Maruyama simulator. Include, in the zip file of the solution, a short word document were you describe accurately the material that you used (in case you can use MathType to edit possible formulas). The process can, and must, be researched on the Internet. The process can be any continuous diffusion process with jumps. Cite accurately the sources you used for your process. You must provide the SDE that you used and the corresponding simulation.
jump diffusion

img source: http://www.wilsonmongwe.co.za/introduction-to-diffusion-and-jump-diffusion-processes-2/

Final ZIPPED files with complete source solutions (must contain the entire folder, with the .sln solution entry file), must be uploaded on Google Drive and must contain your name in the file name: YourName_StatApp.ZIP YourName_SDESim.ZIP.
Do not publish or share the links to the final exam projects. Do not make collaborative work at this exam stage (we had plenty during the course).

When done with the projects, please send me 1 email to the following address: statisticssapienza@gmail.com with the following information (try to keep it short and precise):

-1 name, ID
-2 link to your research and applications blog
-3 links to your 2 final version of projects (1.Stat application and 2.Euler–Maruyama simulator) on Google drive (final ZIPPED solution folder with complete and fully tested source solution, must be uploaded on Google Drive and must contain your name in the 2 file names: YourName_StatApp.ZIP YourName_SDESim.ZIP)
-4 number of "discontinuity penalties" (homeworks not handed on time) accumulated, if any
-5 brief "defense" of your work and study during the course
-6 your final proposed grade (must subtract penalties, if any)
-7 optional. Two words on : How did you find this course ? What did you like and how would you improve it ?

To speed things up, given the large number of students, if your grade proposal will appear comparatively fair - given your researches online and your final projects - I will accept direcly that on the oral exam, otherwise we will go through a more detailed examination for accurate assessment. (The oral exam will be carried out in any case.) When ready, send the email with the listed material and we will make an appointment for the next day to do the oral exam via remote (will use whatsapp, as usual) (obviously this must happen before the official date exam, so that the exam can be verbalized on the due date.)

A word of caution (just in case):
1) If exam application projects are essentially identical, in the sense that apart superficial camuflages, they are obviously from the "same hand", they will all be nullified.
2) Do not book for the exam if you are not adequately prepared. There are few things less more itrritating than students "trying" to pass exams without sufficient preparation or, even worse, trying to cheat using work done by others.

______________________________________________________________________________________________________________

Useful general-purpose free tools

Visual Studio (IDE) https://visualstudio.microsoft.com/it/downloads/ https://visualstudio.microsoft.com/it/vs/older-downloads/ (include C# and VB.NET)
Video Player VLC (video player) https://www.videolan.org/vlc/download-windows.it.html
Notepad++ (edit CSV data files) https://notepad-plus-plus.org/downloads/
OBS Studio, open broadcaster software (to record video with screen and audio/cam) https://obsproject.com/
Autodesk SketchBook (to make drawings) https://sketchbook.com/
MP4Tools (simple mp4 cut/join) https://www.mp4joiner.org/en/

HTML Corrector: https://www.htmlcorrector.com/
HTML Validator: https://www.freeformatter.com/html-validator.html
Spell check: https://spellcheckplus.com/